線形目盛と対数目盛 - Linear Scale and Logarithmic Scale

This is a post written in RMarkdown (*.Rmd) to understand reasons to use logarithmic scales in charts. この記事ではチャートやグラフに対数目盛りを使う目的についてまとめています。Naomi Robbins¹さん、Gregory Kanevsky²さん、Hunkar Ozyasar ³さんの記事を参考にしています。

キーポイント

線形目盛と対数目盛りの違い：

線形目盛（Linear Scale） : 等間隔の幅が一定の量の変化を表している。
対数目盛（Logarithmic Scale） : 等間隔の幅が量の変化率を表している。

対数目盛（Logarithmic Scale）を使うケース⁴：

データが狭い範囲に密集していない時に使う。極端な外れ値があるデータ、広い範囲の値を持をロングテール型のデータをきれいに可視化できる。
対数目盛は量の変化率を示しているので、指数関数的増加や指数関数的減衰が見られるデータの可視化に適している。

金貨のチャート

1885年の秋のある日、アーサー・ドイルは株式仲買店員の友人に稼ぎの一部を預けることにした。大学卒業後、開業した診療所の仕事がやっと軌道に乗りはじめていた。経済的に困っていたわけではなく、資金繰りが苦しい友人を助けるつもりだった。預けたソブリン金貨には複利の利子がつく。「金貨は必ず毎年0.5倍ずつ増えていく」

R言語: 線形目盛

time <- 1:10  # 貯蓄期間
r <- 0.5  # 成長率
a <- 10  # 預けた金貨
y <- a * (1 + r)^time  # 指数関数的な成長, (1+r) is the growth factor
plt <- qplot(seq_along(y), y, xlab = "年数", ylab = "金貨")
plt + scale_y_continuous(breaks = seq(0, 1000, by = 100)) + scale_x_continuous(breaks = seq(0, 
    10, by = 1))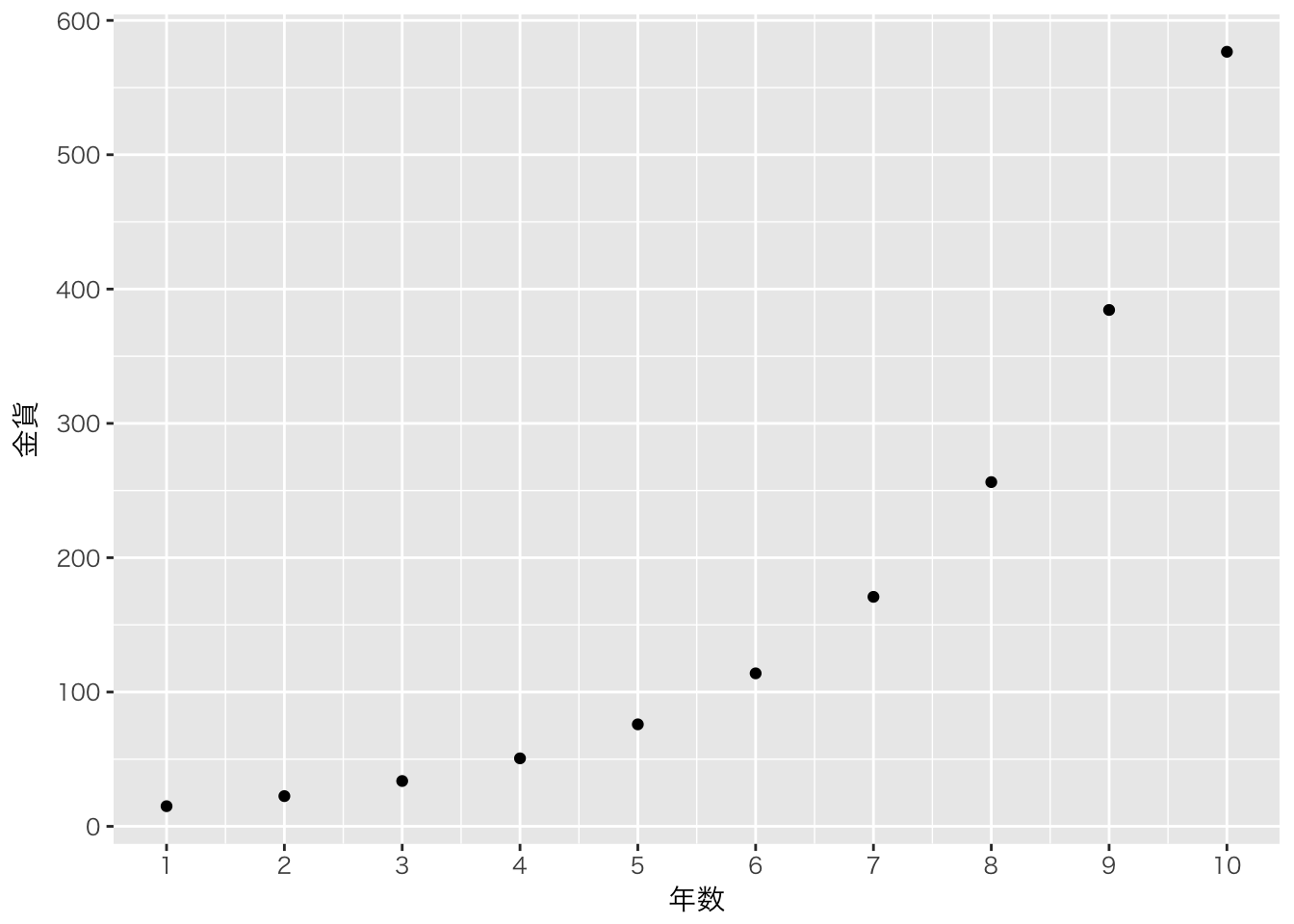

チャート1:金貨と預入期間

10年が経ち、友人が約束した通り預けた金貨は増えていった。

チャート1は、金貨と預入期間の関係を線形目盛で可視化している。垂直軸であるY軸上の等間隔の幅が一定の量の変化を示している。1cmの幅が金貨100枚の増加を表している場合、200枚から300枚への増加も1cmの幅がある。

アーサーは友人に渡された線形目盛のチャートをながめながら、5年目から10年目の金貨の増え方に比べて、1年目から5年目までの金貨の増え方が分かりづらいと思った。アーサーは友人に新しいチャートを用意させることにした。「5年目までの金貨の増え方をもっと分かりやすく見せてくれ」

R言語: 対数目盛

plt <- qplot(seq_along(y), log(y), xlab = "年数", ylab = "log(金貨)")
plt + scale_x_continuous(breaks = seq(0, 10, by = 1))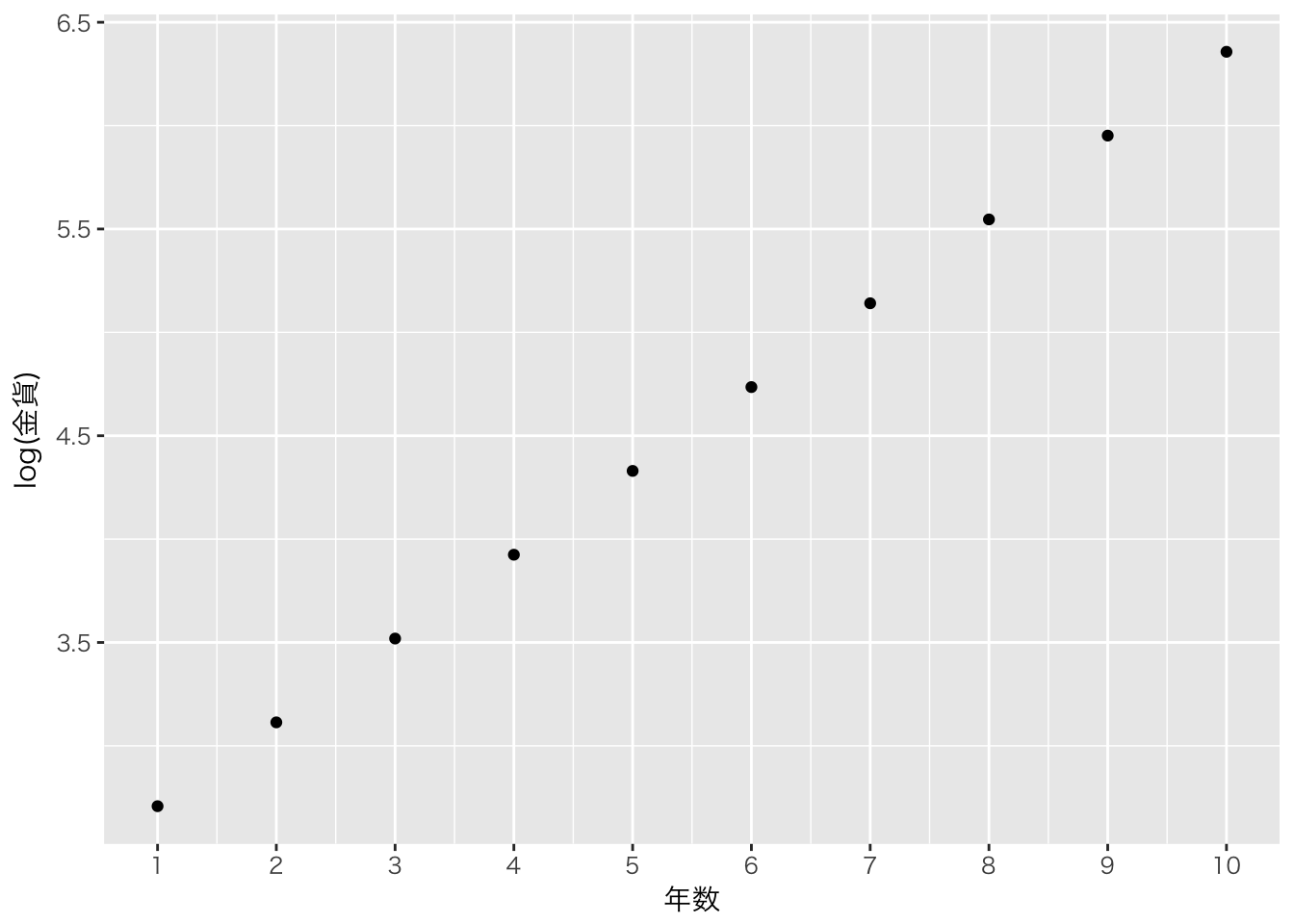

チャート2:金貨と預入期間

友人はアーサーの要望を受けて新しいチャートを用意した。

チャート2は、金貨と預入期間の関係を対数目盛で可視化している。垂直軸であるY軸上の等間隔の幅が量の変化率を示している。1cmの幅が金貨の50%の増加を表している場合、同軸上の異なる位置でも1cmの幅は50%の増加を示している。

金貨は毎年同じ増加率を達成していた。アーサーは友人に渡された対数目盛のチャートを見てとても満足した。一方の軸が対数目盛になっているチャートを片対数(semi-log)チャートと呼ぶ。⁵片対数チャートを見ると増加傾向は毎年同じ比率を保っていることが分かった。

1年目から5年目まではわずかな増加だった金貨は、5年目から10年目にかけて急激に膨れ上がった。そのせいで、チャート1では1年目から5年目までの変化がはっきりしないものになっていた。チャート2ではデータの全体像を正確に捉えることができている。

ベイカー・ストリート